#Computer science

[thewinastudyblog]

some advice i have for future computer science students

as soon as you learn data structures & complexity, run, don’t just walk, RUN to leetcode while the knowledge is still fresh in your mind. your entire career and whether you’ll get a well-paying job vs an average paying job depends on how good you are at leetcode.

build as many projects as you can, and i’m not talking tutorial projects that take a few hours, i’m talking big projects. working on a project for a month or two will get you really far.

if you don’t have an internship, do not waste your summers, learn new technologies, languages, concepts and build projects you can put in your cv.

try to participate in hackathons and coding competitions. it’s okay if you fail, but you’ll learn a lot.

learn how to read documentation. most tutorials don’t even cover a quarter of what a language, framework or software has to offer. the sooner you make reading documentation a habit, the better it is. and yes i know, documentation is long and hard to read. my advice is only read the sections that are relevant to you in the moment. something i also personally do is look at the code examples at the same time as i am reading the paragraphs, it really helps easily absorb the information.

try not to use chatgpt. and if you do, then at least use it for stuff you know you can do yourself and will be able to correct if the bot gets it wrong. using chatgpt is a very slippery slope and the more you use it the less you learn.

the math is important. math teaches you how to reason and how to develop better logical thinking. just because you don’t see yourself using the xyz theorem you’ve learnt anytime in the future doesn’t mean the math is useless.

be prepared to get comfortable with erros, issues, bugs and just problems in general. you’ll be coding 30% of the time and debugging 70% of the time (i’m exaggerating but sometimes it feels like this is the case lol), and that’s okay, it’s how we learn and the sooner you embrace it the better. if you’re someone who easily gets frustrated, then this is a heads up.

learn as you go. there is no such thing as waiting until you know everything before you start on a project. the only way and the best way to learn in this field is practice, so build, build, and build.

these are all the ones i could think of for now. feel free to comment your thoughts and questions <3

[unsheathedpepsipop]

I had an Operating Systems module earlier this year, and it has me unironically typing this stuff into my search bar. Here it is from my search history.

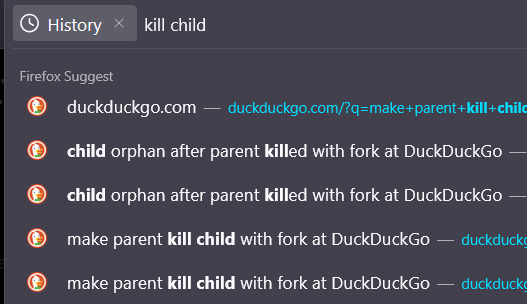
coding got me saying shit like “target the child” “assign its class” “override its inheritance” like the third wife of a dying oil baron discovering his of-age son born out of wedlock

[captaindrewboy]

I hate when I tell people I'm into Comp Sci and programming and they go "ooh there's a lot of money there". I'm not DOING it for the MONEY I'm DOING it because I want to FUCK the COMPUTER!!!!

[devotedlystrangewizard]

i think everyone should program at least once just so you realise just how fucking stupid computers are. because theyre so fucking stupid. a computer wants to be told what to do and exactly that and if you make one typo or forget one detail it starts crying uncontrollably

[allie-leth]

"oh, nevermind, I got it working" - posted 11 years ago, end of thread.

I HATE YOU WITH EVERY FIBER OF MY BEING

[prokopetz]

Wrong: Ada Lovelace invented computer science and immediately tried to use it to cheat at gambling because she was Lord Byron's daughter.

Right: Ada Lovelace invented computer science and immediately tried to use it to cheat at gambling because that was the closest you could get in 1850 to being a Super Mario 64 speedrunner.

[feyosha]

Computers are very simple you see we take the hearts of dead stars and we flatten them into crystal chips and then we etch tiny pathways using concentrated light into the dead star crystal chips and if we etch the pathways just so we can trick the crystals into doing our thinking for us hope this clears things up.

[microwavedmetal]

This is as unhinged as this laptop soon will be

[er-cryptid]

alright nerds--

^tried to include as many as possible

[c-u-c-koo-4-40k]

What should you bring to school?

For the people of Gaza, the memories of days spent in school are distant. But education is not Only a Right but a Duty.

Meet Anas and Ahmad, they are related to Osama Basil, who has his own gofundme.

While managing his own gfm, Osama is also trying to help Anas and Ahmed fund their education somewhere safe, away from the Turmoil in Gaza.

They are Bright Wonderful students who want to pursue careers in computer business and medicine!

Please give some time to this Verified campaign!

Current Funding

€4,870 / €29,000

~16% Funded

Tag List for Reach DM me for Removal

And to others putting me in mentions I am So Sorry I'm not getting to many of them, I'm trying to balance between DM campaigns, ask campaigns and the mentions I get each day.

@a-shade-of-blue @sunnylittledragon

@selflovejolteon @virovac

@frustrated-froglet @qattdraws @heydreamchild

@amvs @boosting-donations

@sweet-honey-bunnies

@dyspunktional-leviathan

@nobelgasxenon

@zone0neko

@comrademango

[some-douchey-techbro]

In programming, being killed and being executed mean the exact opposite things

[1863-project]

Okay, I've been having trouble finding this, but I know it existed because my dad showed it to me multiple times.

My dad, recently retired, had a 40+-year IT career starting in the 1980s. (His biggest claim to fame is writing the programming for the printer driver for a program called PC Paintbrush, which was purchased by Microsoft and became Microsoft Paint, but I digress.) When I was a kid, he showed me an Easter egg snuck into an early Windows operating system where if you typed in a certain command an animation of Bill Gates as Godzilla would show up and start using his breath to zap people into Windows logos. I know it existed and isn't something I imagined because he pulled it up for me upon request multiple times, but seeing as this was the 1990s and I was a child I didn't have the details, like what OS it was. (My best guess would be 95 or 98.) I just want to see if I can recover that animation and document its existence somehow, but I haven't been able to find anyone else looking for it or who knows about it.

Any leads or information you might have would be super helpful! Thanks in advance!

UPDATE FROM DAD: it was on the desktop, you got it to show up by inputting a key sequence that he doesn't remember, and he's pretty sure it was Windows 98.

[nasa]

LaRue Burbank, mathematician and computer, is just one of the many women who were instrumental to NASA missions.

4 Little Known Women Who Made Huge Contributions to NASA

Women have always played a significant role at NASA and its predecessor NACA, although for much of the agency’s history, they received neither the praise nor recognition that their contributions deserved. To celebrate Women’s History Month – and properly highlight some of the little-known women-led accomplishments of NASA’s early history – our archivists gathered the stories of four women whose work was critical to NASA’s success and paved the way for future generations.

LaRue Burbank: One of the Women Who Helped Land a Man on the Moon

LaRue Burbank was a trailblazing mathematician at NASA. Hired in 1954 at Langley Memorial Aeronautical Laboratory (now NASA’s Langley Research Center), she, like many other young women at NACA, the predecessor to NASA, had a bachelor's degree in mathematics. But unlike most, she also had a physics degree. For the next four years, she worked as a "human computer," conducting complex data analyses for engineers using calculators, slide rules, and other instruments. After NASA's founding, she continued this vital work for Project Mercury.

In 1962, she transferred to the newly established Manned Spacecraft Center (now NASA’s Johnson Space Center) in Houston, becoming one of the few female professionals and managers there.  Her expertise in electronics engineering led her to develop critical display systems used by flight controllers in Mission Control to monitor spacecraft during missions. Her work on the Apollo missions was vital to achieving President Kennedy's goal of landing a man on the Moon.

Eilene Galloway: How NASA became… NASA

Eilene Galloway wasn't a NASA employee, but she played a huge role in its very creation. In 1957, after the Soviet Union launched Sputnik, Senator Richard Russell Jr. called on Galloway, an expert on the Atomic Energy Act, to write a report on the U.S. response to the space race. Initially, legislators aimed to essentially re-write the Atomic Energy Act to handle the U.S. space goals. However, Galloway argued that the existing military framework wouldn't suffice – a new agency was needed to oversee both military and civilian aspects of space exploration. This included not just defense, but also meteorology, communications, and international cooperation.

Her work on the National Aeronautics and Space Act ensured NASA had the power to accomplish all these goals, without limitations from the Department of Defense or restrictions on international agreements. Galloway is even to thank for the name "National Aeronautics and Space Administration", as initially NASA was to be called “National Aeronautics and Space Agency” which was deemed to not carry enough weight and status for the wide-ranging role that NASA was to fill.

Barbara Scott: The “Star Trek Nerd” Who Led Our Understanding of the Stars

A self-described "Star Trek nerd," Barbara Scott's passion for space wasn't steered toward engineering by her guidance counselor. But that didn't stop her!  Fueled by her love of math and computer science, she landed at Goddard Spaceflight Center in 1977.  One of the first women working on flight software, Barbara's coding skills became instrumental on missions like the International Ultraviolet Explorer (IUE) and the Thermal Canister Experiment on the Space Shuttle's STS-3.  For the final decade of her impressive career, Scott managed the flight software for the iconic Hubble Space Telescope, a testament to her dedication to space exploration.

Dr. Claire Parkinson: An Early Pioneer in Climate Science Whose Work is Still Saving Lives

Dr. Claire Parkinson's love of math blossomed into a passion for climate science. Inspired by the Moon landing, and the fight for civil rights, she pursued a graduate degree in climatology.  In 1978, her talents landed her at Goddard, where she continued her research on sea ice modeling. But Parkinson's impact goes beyond theory.  She began analyzing satellite data, leading to a groundbreaking discovery: a decline in Arctic sea ice coverage between 1973 and 1987. This critical finding caught the attention of Senator Al Gore, highlighting the urgency of climate change.

Parkinson's leadership extended beyond research.  As Project Scientist for the Aqua satellite, she championed making its data freely available. This real-time information has benefitted countless projects, from wildfire management to weather forecasting, even aiding in monitoring the COVID-19 pandemic. Parkinson's dedication to understanding sea ice patterns and the impact of climate change continues to be a valuable resource for our planet.

Make sure to follow us on Tumblr for your regular dose of space! 

[cheekios]

Rationing Insulin.

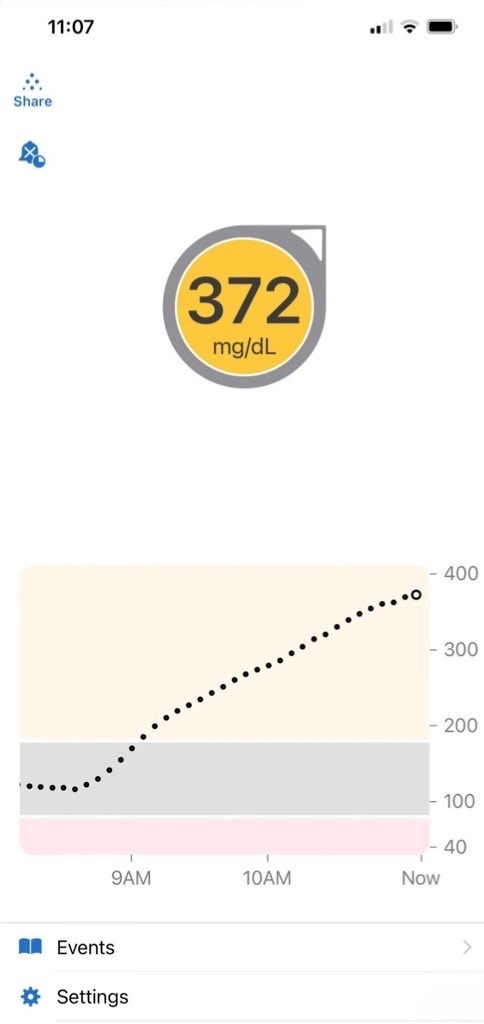
Blood sugar reading this morning. The average blood sugar reading should be between 60mg/dl - 100mg/dl. I am terrified of not being able to administer my insulin simply because I was too poor to afford it. I am strongly in need of community help.

CA: $HushEmu

PP: emuslayter@gmail.com

I am happy to announce I raised $33 🎉 I only need $417 to get my prescription

[prokopetz]

I think more academic programs should let you write a novel as your thesis project, particularly outside the fine arts. Just imagine the kind of bullshit that would result if they let you write a novel for your master's degree in computer science.